前
有幸的划水了第一波腾讯的笔试。虽说整体过程的题目还是算容易,不过实际上还是由不少的困难。这次是自己的一点总结帖。
离线开锁 声波锁 和 2FA 技术。
二叉树 (BinTree)
基本结构
定义:
二叉树在图论中是这样定义的:二叉树是一个连通的无环图,并且每一个顶点的度不大于3 。有根二叉树还要满足根结点的度不大于2。有了根结点之后,每个顶点定义了唯一的父结点,和最多2个子结点。然而,没有足够的信息来区分左结点和右结点。如果不考虑连通性,允许图中有多个连通分量,这样的结构叫做森林。
二叉树中每个节点都是他的左右字数的前驱,左右子树也是器根节点的后继。
名词:words
- 兄弟 具有同一父节点的节点
- 祖先/子孙 如果y在x为根节点的子树中且 y <> x 则x 是y的祖先
- 层数 规定根层数为0,其余结点层数等于其父节点层数加一。
- 度数 节点的飞控字数个数即为树的度。
- 树的高度 所有节点中的最大的层数称为二叉树的高度。
- 树叶/分支 左右子树均为空的结点称为树叶,否则是称为分支节点。
- 特殊二叉树
- 满二叉树 如果任意节点都有两棵非空子树或者树叶。
- 完全二叉树 只有最下面的两侧的节点度数小于2 其他的层各节点的度数等于2 。

性质:
- 第i层最多有 2^i个节点
数据存储结构
顺序存储结构
对应一个二叉树,我们使用语言实现它
#define Maxsize 100 //假设一维数组最多存放100个元素typedef char Datatype; //假设二叉树元素的数据类型为字符typedef struct{ Datatype bt[Maxsize]; int btnum;}Btseq;这里的顺序存储结构,实际上是可以看作,是吧二叉树压扁,投影在一个数组里。
如上图 A是根,B是其左节点,C是其右节点。那么我们在顺序存储中得到的数组的内容是:
ABCD^EFGH^^^I^^链式存储结构
这里是使用链式结构,具体代码如下:
typedef char Datatype; //定义二叉树元素的数据类型为字符typedef struct node //定义结点由数据域,左右指针组成{ Datatype data; struct node *lchild,*rchild;}Bitree;这个结构是见解明了了。一个三个元素,本身的数据。左子树和右子树。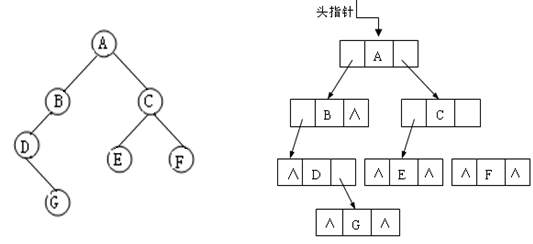
二叉树的遍历
这个问题算是一个超级基本的问题了,基本上是逃不过的。不过之前的印象深刻滚瓜烂熟。突然遇到还是懵逼一会。所以及时总结,加强记忆。
通常来说对二叉树的遍历有以下的三种方式。
- NLR:前序遍历(Preorder Traversal 亦称(先序遍历)) (根左右)
- LNR:中序遍历(Inorder Traversal) (左根右)
- LRN:后序遍历(Postorder Traversal) (左右根)
这里采用第二种存储方式.如果我们对其孩子节点进行一次访问,那么我们对其指针进行一次指向即可。
node lChild = *this->lchild;这里采用递归的方法。对整个的二叉树的结构进行遍历,并打印其值
前序遍历
void preTraversal(node* root){cout << root->data; //先进行根操作if(root->lchild != NULL) // 实际上的遍历的类型在这里是其操作顺序决定的, preTraversal(root->lchild);if(root->rchild != NULL) preTraversal(root->rchild);}中序遍历
void preTraversal(node* root){if(root->lchild != NULL) // 实际上的遍历的类型在这里是其操作顺序决定的, preTraversal(root->lchild);cout << root->data; // 当上面的递归开始返回的时候,第一次执行的是我们的左叶子节点 // 当第一次返回后,现在是该节点的父节点,即根节点if(root->rchild != NULL) // 之后继续查找右节点 preTraversal(root->rchild); // 这次调用,会打印右节点的值}后序遍历
void preTraversal(node* root){if(root->lchild != NULL) // 实际上的遍历的类型在这里是其操作顺序决定的, preTraversal(root->lchild); if(root->rchild != NULL) preTraversal(root->rchild);cout << root->data; }这里递归的思路是一定要清楚,如果我们画出了调用栈,那个更清楚。
Q&A
Q: 某二叉树前序遍历访问顺序是abdgcefh,中序遍历访问顺序是dgbaechf,则后序遍历的结点访问顺序是多少?
A: 这个是超经典的一类问题了,可能考试都要考它。实际上我们的分析,思路如下:我们要做到的是还原二叉树。从第一个我们可以得到 根节点是 a,中序遍历的话是左根右的顺序,所以我们可以找到在中续遍历中找到a,把其分为agb,和aechf两个子树。
之后周而复始,bdg也是根左右。cefh也是根左右。之后c取出分e,hf两个子树。
